Andreagiovanni Reina - Centre for the Advanced Study of Collective Behaviour, Konstanz & Max Planck Institute of Animal Behavior

Andreagiovanni Reina - Sheffield Robotics - Kilobots

Andreagiovanni Reina - Sheffield Robotics - Kilobots ARK - Talamali

Engineering distributed decision making

I am best known for my work in the field of engineering distributed decision-making, which aims to design artificial swarm systems capable of making consensus decisions. I employ a multiscale modelling technique to deeply understand the system before implementing it on swarms composed of hundreds of robots. I have been invited by several institutes for to give lectures on this topic, illustrate the techniques I developed, and showcase robot swarm results.

A design pattern for decentralised decision making

Each day, our world is more and more connected and the number of intelligent (smart) devices that interact with each other is exponentially growing. In general, large scale distributed systems, also called swarm systems, are becoming pervasive in several domains. Such systems are composed of a large number of autonomous agents (e.g. robots, or smart devices) with typically limited capabilities, that coordinate and cooperate to perform a common task. A peculiar characteristic of such systems is the absence of any central leader. The underlying principle that allows a decentralised swarm to coherently operate is called self-organisation. A self-organising process results in an emerging swarm behaviour that is often difficult to design, predict, and it may easily go out of the engineer’s control. While, the engineering of decentralised swarm systems may be very arduous and challenging, diverse domains would benefit from a reliable implementation of such systems. Some examples are nano-robots for surgical operations, cooperative spectrum allocation in cognitive radio networks, or collective exploration in remote or unaccessible locations, such as other planets or disaster areas.

While a general-purpose design methodology for distributed systems may be unworkable, I believe that a viable solution is the definition of design patterns for specific class of problems. The underlying idea is to put in use the knowledge of well-understood macroscopic models of distributed systems to formalise the implementation steps of engineered systems. A design pattern offers a set of models to analyse and predict the system behaviour at the macroscopic level, and a set of rules and guidelines to allow a multi-agent implementation that quantitatively link macroscopic predictions to multi-agent outcome. The main novel contribution consists in providing the engineer with a top-down implementation methodology that allows full control over the system dynamics and accurate performance guarantees. I propose a design pattern for collective decision making inspired by the models conceived to describe the nest site selection process in honeybee swarms.

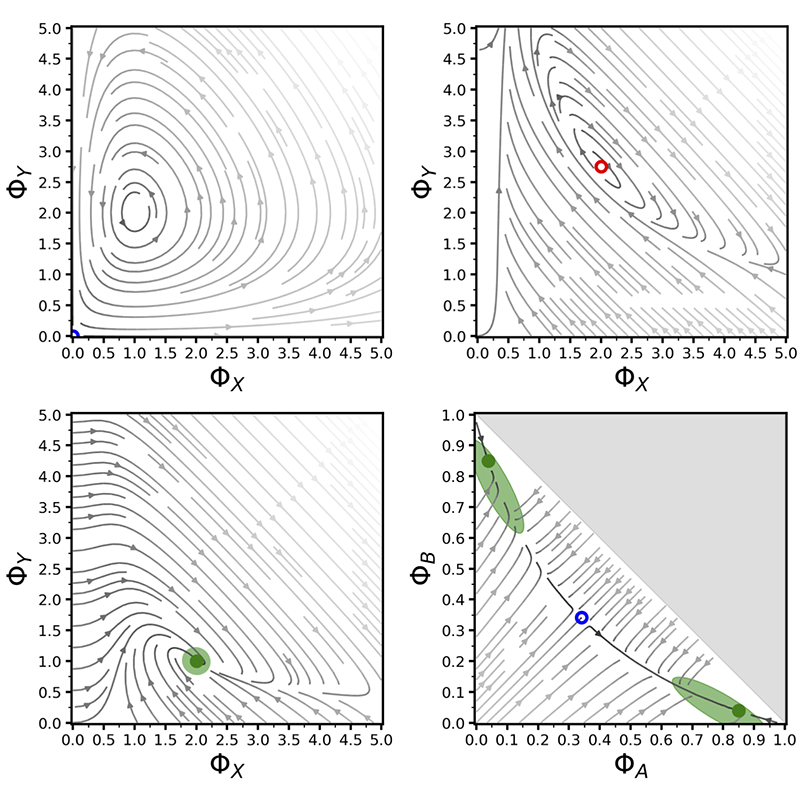
The video above shows an implementation of the design pattern on a swarm of simulated e-puck robots. The robot swarm is asked to select (and exploit) the target area (black spot) that is the closest to the home area (gray spot). Each robot has limited sensing and communication capabilities and the task is challenging due to the absence of a central leader coordinating the operation. Exploiting the design pattern, the designer is provided with complete control and accurate predictions of the swarm dynamics. The agreement between macroscopic dynamics and multiagent implementation is shown in the figures here above. The density maps and the histograms report multi-agent simulation results, while the bifurcation lines and phase portrait describe the macroscopic dynamics (green unstable and blue stable). See cited papers below for more info.

Best-of-n decisions

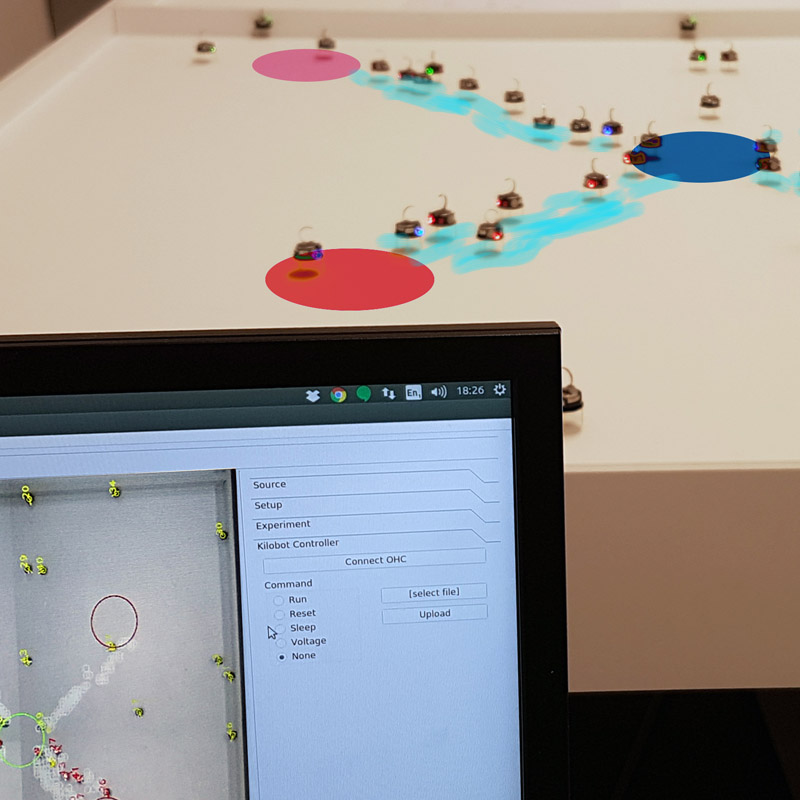
One relevant decision problem is the best-of-n problem, in which the goal is to select the best option among a set of alternatives. In my studies, individual robots are simplistic as they only perform diffusive search, make local noisy estimates of the options’ quality, and exchange information with near neighbours. My main contribution has been to design decentralised algorithms, inspired by house-hunting honeybees, to efficiently aggregate noisy estimations of the individual robots in order to reach a consensus for the best option. The design of the algorithms has been based on principled multiscale modelling which consists in a combination of statistical physics techniques, computational models, and multiagent simulations. In particular, we link the macroscopic dynamics of the swarm, which we describe through ODEs and master equations, to the microscopic behaviour executed by the individ- ual robots. In my studies, I perform a gradual implementation starting with non-spatial simulations, passing to self-propelled particles that allow investigations on the effect of spatial correlations and spatial biases, moving to physics-based simulations that allow quantifying the effect of physical embodiment and interference, finally reaching robot swarm experiments that confirm the functioning of the algorithm on physical devices affected by noise and hardware failures. I conducted most of my robot experiments with the Kilobots which are minimalistic robots widespread for swarm robotics studies in academia.

A. Reina, T. Bose, V. Trianni, J.A.R. Marshall. Effects of Spatiality on Value-Sensitive Decisions Made by Robot Swarms. In Proceedings of the 13th International Symposium on Distributed Autonomous Robotic Systems (DARS 2016). STAR Series, Springer, Berlin, Germany, 2016.
A. Reina, G. Valentini, C. Fernández-Oto, M. Dorigo and V. Trianni. A design pattern for decentralised decision making. PLoS ONE 10(10): e0140950, 2015.
A. Reina, R. Miletitch, M. Dorigo and V. Trianni. A quantitative micro-macro link for collective decision: the shortest path discovery/selection example. Swarm Intelligence, 9(2-3):75-102, 2015.
A. Reina. Engineering swarm systems: A design pattern for the best-of-n decision problem, PhD Thesis, IRIDIA, Ecole Polytechnique de Bruxelles, Université Libre de Bruxelles, Belgium, 2016.
A. Reina, M. Dorigo and V. Trianni. Towards a Cognitive Design Pattern for Collective Decision-Making. In Proceedings of 9th International Conference on Swarm Intelligence (ANTS), LNCS 8667, pages 194-205. Springer, Berlin, Germany, 2014.
A. Reina, M. Dorigo, and V. Trianni. Collective decision making in distributed systems inspired by honeybees behaviour. In Proceedings of 13th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), pages 1421–1422. IFAAMAS, New York, 2014.

Breaking the decision-deadlock

In collective decisions in which the options have no quality or all have the same quality, the swarm should agree on one option and avoid to remain undecided with subgroups each favouring a different option. Through my research, I showed that while some decision models cannot break the decision deadlock and remain split into subgroups, other models prove able to show deadlock-breaking dynamics and reach consensus for one of the available options. Some models may also display value-sensitive dynamics by which the group selectively breaks or maintains the decision deadlock as a function of the opinion’s quality. If the equal-quality options have a quality above a given threshold, the group makes a decision, otherwise it refrains from deciding until a sufficient-quality option becomes available. Through my analyses, I show that these systems' dynamics are often determined by the balance between individual and social information.

The video below shows a swarm of 150 robots that take a value-sensitive decision. The robots follow a set of rules that are inspired by the behaviour of house-hunting honeybees. See the cited papers below for more information.

A. Reina, T. Bose, V. Trianni, J.A.R. Marshall. Effects of Spatiality on Value-Sensitive Decisions Made by Robot Swarms. In Proceedings of the 13th International Symposium on Distributed Autonomous Robotic Systems (DARS 2016). STAR Series, Springer, Berlin, Germany, 2016.
I. Rausch, A. Reina, P. Simoens, Y. Khaluf. Coherent collective behaviour emerging from decentralised balancing of social feedback and noise. Swarm Intelligence 13(3-4): 321-345, 2019.

Minimal naming game

The minimal naming game is a model that describes basic mechanisms of how social conventions may form in a population without centralised coordination. In the naming game, a network of locally interacting individuals can spontaneously self-organise to reach global agreement. We tested how the naming game dynamics would change if we would move from computer simulations of self-propelled particles to the implementation on a swarm of physical robots.